Wektor zapisywany jako liczba - teoria
Spis treści – czyli co tutaj znajdziesz:
(przydatne info – jak klikniesz któryś zielony napis poniżej, to od razu cię tam przeniesie)
Wstęp - o czym dzisiaj?
Wyobraź sobie taki scenariusz. Jest jesień, za oknami ciemno, a deszcz rytmicznie uderza w szybę. W powietrzu unosi się zapach świeżo upieczonej szarlotki. Ciągnie cię, żeby pobiec po ciasto do kuchni, ale najpierw musisz zrobić ostatnie zadanie z fizyki. Otwierasz książkę i czytasz „Ciało A porusza się z prędkością $5\frac{\text{m}}{s}$…”.

Stwórzmy sytuację - tradycyjny sposób zapisu
Stwórzmy sobie układ współrzędnych i umieśćmy w nim żółwia. Początkowy wektor położenia żółwia to $\vec{r}_{0}=[-5,0] \text{m}$, ale idzie przed siebie z prędkością $\vec{v}=[20,0]\frac{\text{m}}{\text{h}}$.
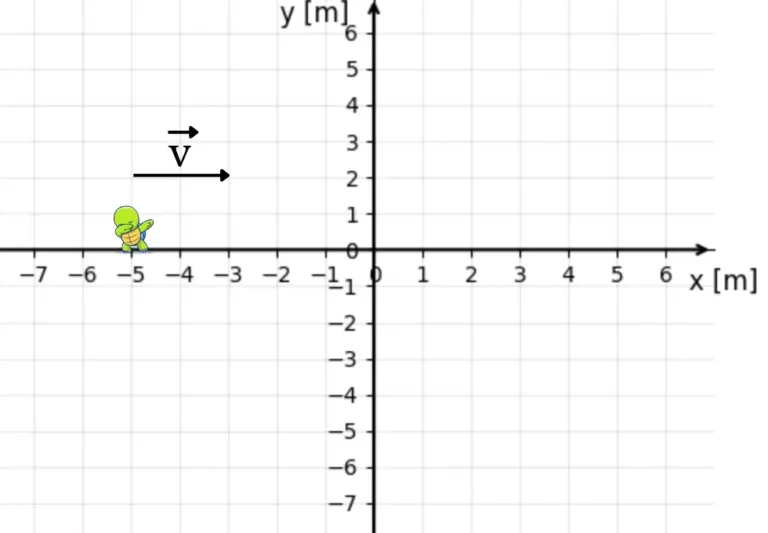
Jeżeli chcemy dowiedzieć się gdzie będzie on za jedną godzinę możemy skorzystać ze wzoru na prędkość (wytłumaczenie tego wzoru znajdziesz tutaj)
$\vec{v}=\frac{\Delta\vec{r}}{t}=\frac{\vec{r}_{k}-\vec{r}_{0}}{t}$
Przekształćmy go do poniższej postaci (jeśli przekształcanie wzorów sprawia ci problem, zajrzyj tutaj)
$\vec{r}_{k}=\vec{v}t+\vec{r}_{0}$
Spójrz, że znamy wartości wszystkiego po prawej stronie znaku równa się, więc możemy już podstawić dane i policzyć wektor położenia końcowego
$\vec{r}_{k}=[20,0]\frac{\text{m}}{\text{h}}\cdot1\text{h}+[-5,0]\text{m}$
$\vec{r}_{k}=[15,0]\text{m}$
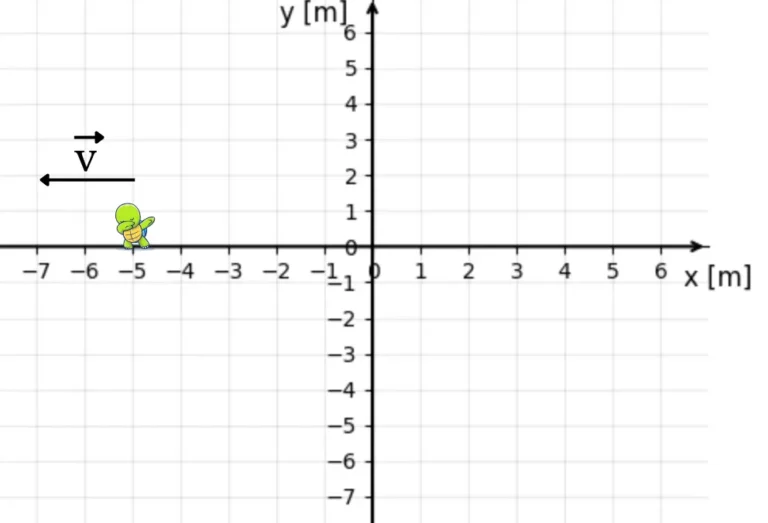
A gdyby żółw szedł z prędkością $\vec{v}=[-20,0]\frac{\text{m}}{\text{h}}$, to jakie będzie położenie żółwia po godzinie?
To tutaj znowu możemy skorzystać z naszego wzoru
$\vec{r}_{k}=\vec{v}t+\vec{r}_{0}$
ponieważ zmieniły się tylko wartości wektorów, a nie rozkminiane zagadnienie (niech żyje wyprowadzanie wzorów końcowych). Więc podstawmy dane i policzmy
$\vec{r}_{k}=[-20,0]\frac{\text{m}}{\text{h}}\cdot1\text{h}+[-5,0]\text{m}$
$\vec{r}_{k}=[-25,0]\text{m}$
Czy da radę prościej? - wprowadzenie do uproszczonego zapisu
Zauważ, że za każdym razem w obliczeniach druga składowa była równa zero i totalnie nic się tam nie zmieniało. Więc przepisywanie tego było monotonne i może wydawać się bezcelowe.

Może łatwiej byłoby olać tą drugą składową? Okazuje się, że niektórzy na to pytanie odpowiedzieliby ,,To jest genialne. Zróbmy tak”. I naszą początkową historie o żółwiu opisaliby tak:
Stwórzmy sobie układ współrzędnych i umieśćmy w nim żółwia. Początkowy wektor położenia żółwia to $\vec{r}_{0}=-5\text{m}$, ale idzie przed siebie z prędkością $\vec{v}=20\frac{\text{m}}{\text{h}}$
A kiedy nasz żółw miałby prędkość $\vec{v}=[-20,0]\frac{\text{m}}{\text{h}}$, to by zapisali:
Stwórzmy sobie układ współrzędnych i umieśćmy w nim żółwia. Początkowy wektor położenia żółwia to $\vec{r}_{0}=-5\text{m}$, ale idzie przed siebie z prędkością $\vec{v}=-20\frac{\text{m}}{\text{h}}$
Jest tylko jedno, małe, maciupkie ,,ale”. Zaproponowany tu uproszczony zapis nie mówi nam, czy ruch odbywa się wzdłuż osi x-owej, czy osi y-owej. Bo pomyśl, nasz żółw mógł być na początku na $\vec{r}_{0}=[0,-5]\text{m}$ i poruszać się z prędkością $\vec{v}=[0,20]\frac{\text{m}}{\text{h}}$. Tutaj to pierwsza składowa jest nie potrzebna. Co możemy zrobić z tym fantem? Jak zrobić, żeby było to czytelne?
Zadanie na teraz - zwiększenie czytelności zapisu
Wiemy, że wektor położenia $\vec{r}$ możemy zapisać tak (jeżeli tego nie wiesz, to wskakuj tutaj)
$\vec{r}=[r_{x},r_{y}]$,
gdzie $r_{x}$ to x-owa składowa położenia, a $r_{y}$ to y-owa składowa położenia. Więc jeżeli wektor położenia żółwia to $\vec{r}=[-5,0]\text{m}$, to w uproszeniu moglibyśmy napisać, że jego położenie to $r_{x}=-5\text{m}$. Teraz łatwo ogarnąć, że żółw jest na osi x-ów. Dla niektórych nadal jest to zbyt rozbudowany zapis, bo trzeba pamiętać by pisać literkę r. Dlatego w najbardziej uproszczonym zapisie będziemy pisać, że początkowe położenie żółwia to $x=-5\text{m}$, a jeżeli żółw byłby na osi y-owej to położenie jego zapisalibyśmy jako $y=-5\text{m}$. Proste, co nie?

Podsumowanie
W wielu książkach, czy zbiorach zadań możemy znaleźć uproszczony zapis. Poniższe dwa rysunki myślę, że dokładnie wyjaśniają o co z nim chodzi. W końcu jeden rysunek to podobno więcej niż 1000 słów. To w takim razie dwa rysunki to już w ogóle ogrom słów xD
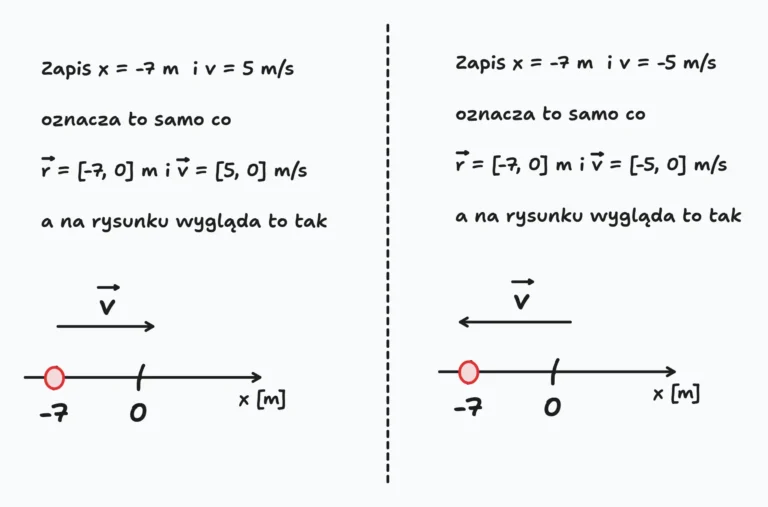
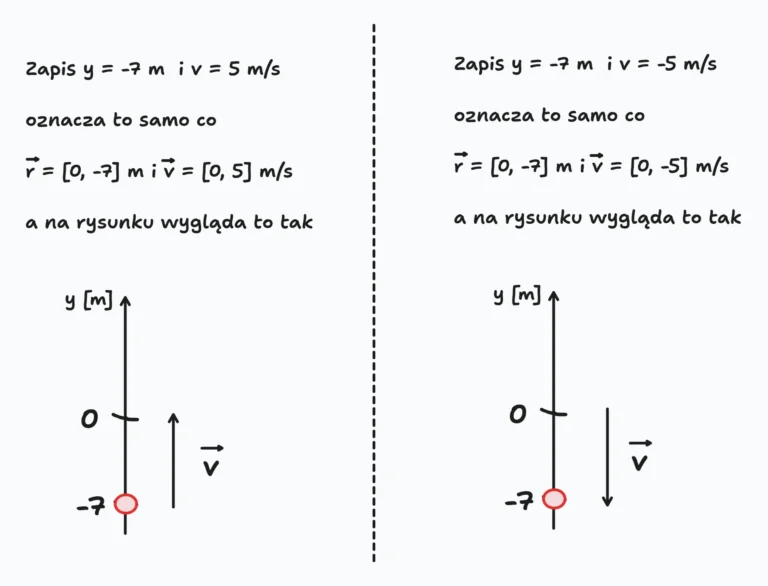
Zwróć uwagę, że we wszystkich 4 opcjach na tych rysunkach zawsze jest napisane v i to jak należy rozumieć ten zapis zależy od kontekstu. Ale myślę, że bez problemu to ogarniesz 😀
Taki uproszczony sposób zapisu ludzie używają również do innych wektorów takich jak np. przyspieszenie, czy siła (do tego dojdziemy za jakiś czas). Ale pamiętaj, to jest uproszczenie i nie wszyscy je uznają. Więc przed użyciem skonsultuj to z nauczycielem bądź wykładowcą, gdyż każde uproszczenie niewłaściwie stosowane zagraża twojej ocenie.
A jeżeli tu już wszystko jest dla ciebie jasne to wskakuj do quizu.
