Ruch jednostajny prostoliniowy - teoria
Spis treści – czyli co tutaj znajdziesz:
(przydatne info – jak klikniesz któryś zielony napis poniżej, to od razu cię tam przeniesie)
Wstęp - stwórzmy abstrakcyjną sytuację
Wyobraźmy sobie taki koszmar. Budzisz się i z zaskoczeniem patrzysz na dziwną lampę leżącą na twojej poduszce. Nie wiedząc o co chodzi, przyglądasz się jej i wtedy wyskakuje z niej dżin, mówiący, że może spełnić jedno twoje życzenie. Dopiero się obudziłeś, więc mówisz pierwsze co ci przyszło do głowy:
- Chcę przeżyć życie poruszając się ruchem jednostajnie prostoliniowym
Dżin ma spore zdziwko, ale nie płacą mu za zadawanie pytań, tylko za spełnianie życzeń. Pstryka i twoje życie właśnie staje się koszmarem.

Ruch jednostajny prostoliniowy - czyli kiedy nic się nie zmienia
Ruch jednostajny prostoliniowy składa się z dwóch słów, które go opisują. Spróbujmy je rozkminić.

Pierwsze – jednostajny. W skrócie mówiąc. Co sekundę musisz przejść dokładnie taką samą drogę. I tak już cały, CAAAŁY czas. Nie ma zwalniania i nie ma przyspieszania. Twoja szybkość musi być stała. Więc po tym życzeniu u dżina musisz nauczyć się spać i jeść idąc, bo już nigdy się nie zatrzymasz. No chyba, że twoja szybkość na początku to było całe okrągłe zero. To wtedy gratulacje, zamieniasz się w skałę, bo już nigdy nie możesz się ruszyć.

To jednak nie koniec atrakcji. Mamy jeszcze drugie słowo – prostoliniowy. Jeśli masz się poruszać ruchem prostoliniowym to musisz iść cały czas wzdłuż jednej prostej. Skręcanie? Zapomnij, to nie tutaj.
W rezultacie, po takim życzeniu u dżina już całe życie zasuwasz z tą samą szybkością i to jeszcze wciąż przed siebie, bez skręcania. To wszystko można też powiedzieć prościej. Twoja prędkość $\vec{v}$ musi być stała, czyli $\vec{v}=\text{const}$.
No nie oszukujmy się, nie brzmi to jak najlepsza opcja na świecie. Ba, zaryzykowałbym nawet stwierdzenia, że nie jest to w pierwszej połowie fajnych rzeczy, które można robić podczas życia. Ale spróbujmy poszukać jakiś zalet tej sytuacji.

Konsekwentnie przed siebie - tyle drogi pokonamy
Skoro poruszasz się wciąż tak samo szybko, np. z szybkością $v$ to obliczenie drogi $s$, którą pokonałeś jest banalnie proste. Wystarczy wiedzieć jak długo się poruszałeś, czyli poznać czas ruchu $t$ i pomnożyć szybkość z czasem
$s=vt$
Więc skoro masz już całe życie ruszać się tak samo szybko, to twój czas ruchu będzie już ogromnie wielki. W rezultacie pokonasz ogromnie dużą drogę. Gdzie zalety tego? Jak się postarasz to może zapiszą cię do księgi Guinnessa, a i lekarze będą z ciebie dumni, bo będziesz pewnie robić ponad 10 tysięcy kroków dziennie xD

Nie zapominajmy o przemieszczeniu!
Widzimy już jasno jak działa sytuacja z drogą $s$. Pamiętamy jednak, że do opisu zachowania się ciała używamy też wektora przemieszczenia $\Delta \vec{r}$.
Wiemy, że skoro poruszasz się ruchem jednostajnym prostoliniowym, to na pewno poruszasz się wzdłuż jednej prostej. Niech tą prostą będzie oś x, bo czemu by nie. Trzeba sobie życie upraszczać. Kiedy ciało porusza się wzdłuż jednej osi, to możemy skorzystać z uproszczonego zapisu przemieszczenia (więcej tutaj) i zamiast o $\Delta \vec{r}$ będziemy mówić o $\Delta x$.
To co z tym położeniem? Z definicji prędkości możemy zapisać
$\vec{v}=\frac{\Delta\vec{r}}{t}$
czyli po uproszczeniu do ruchu wzdłuż jednej prostej
$v=\frac{\Delta x}{t}$
Zanim pójdziemy dalej, przypomnijmy sobie, że $\Delta x$ to przemieszczenie, czyli o ile metrów się przemieściłeś. Liczymy to jako różnica położenia końcowego $x_k$ i położenia początkowego $x_0$
$\Delta x=x_k-x_0$.
Jeżeli połączymy ostatnie dwie zależności dostaniemy
$v=\frac{x_k-x_0}{t}$
Wyznaczmy sobie $x_k$ (jeżeli nie wiesz jak to się robi zajrzyj tutaj)
$x_k=x_0+vt$
No i elegancko. Teraz łatwo możemy rozkminić, gdzie się znajdujesz. Musimy wiedzieć tylko, jak daleko od punktu odniesienia byłeś, mówiąc życzenie (czyli musimy znać $x_0$) oraz jak długo już idziesz (czyli $t$) i z jaką prędkością (v – tutaj pamiętaj, że to może być zarówno dodatnie (kiedy idziesz zgodnie z osią), jak i ujemne (kiedy idziesz w drugą stronę)).
Spróbujmy ogarnnąć to przemieszczenie na przykładzie
Załóżmy, że cała zabawa z dżinem zaczęła się 6 metrów na prawo od układu odniesienia. Czyli $x_0=6\text{m}$. Po czarze dżina postanowiłeś iść z prędkością $v=-3\frac{\text{m}}{\text{s}}$. A więc widzimy, że idziesz w lewo.
Policzmy, gdzie jesteś po 3 sekundach. Zrobimy to wstawiając po prostu liczby do wzoru
$x_k=x_0+vt$
$x_k=6\text{m}+(-3\frac{\text{m}}{\text{s}})\cdot 3\text{s}$
$x_k=-3\text{m}$
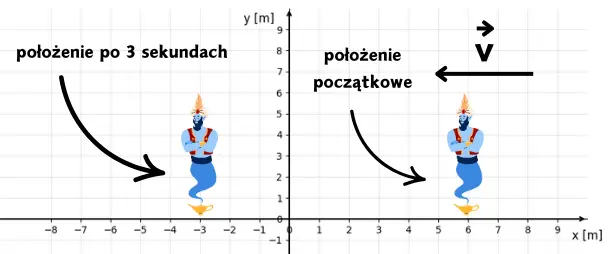
Co znaczy taki wynik? Otóż oznacza on, że po trzech sekundach ruchu jesteś 3 metry na lewo od punktu odniesienia.
I to w sumie tyle z tego przemieszczenia. Nie było tak źle, co nie?
Podsumowując - prędkość musi być stała
Jak widzisz, ruch jednostajnie prostoliniowy nie jest skomplikowanym tworem. I może nie polecałbym go używać non stop, bo jednak skręcanie, czy zmiany szybkości są fajne. Ale używanie go w jakiś krótszych przedziałach czasu niż całe życie, już brzmi znacznie przyjemniej.
A w następnej części pobawimy się tym ruchem jeszcze trochę, bo porobimy sobie wykresiki.
