Czym jest szybkość i prędkość? - teoria
Spis treści – czyli co tutaj znajdziesz:
(przydatne info – jak klikniesz któryś zielony napis poniżej, to od razu cię tam przeniesie)
Wspominki time - o czym rozmawialiśmy ostatnio?
Ostatnio zastanawialiśmy się, w jaki sposób opisywać zmianę położenia ciała (patrz tutaj) i nie powiem, wyszło nam to znakomicie. Wypełniliśmy nasz słownik fizyczny nowymi fancy słowami i uzupełniliśmy tabliczki wzorów o nowe okazy.

Teraz przyszedł czas na kolejną aktualizację, którą zaczniemy pytaniem:
„Ile czasu zajęło przeniesienie się z miejsca początkowego do końcowego?”
Czas - odwieczny kompan
Pytanie wydaje się trywialne, bo przecież wystarczy wziąć stoper. I kiedy ciało zaczyna ruch, włączyć go, a kiedy dotrze na miejsce to wyłączyć. A na końcu najtrudniejsze, odczytać wynik z urządzenia. Tylko, czy rzeczywiście to jest takie proste? Okazuje się, że… tak. Jest to dokładnie tak proste. A to co zmierzymy będzie czasem ruchu oznaczanym literką $t$ od angielskiego słowa time. Podstawową jednostką czasu są sekundy oznaczane jako s. Ale…
Zawsze jest jakieś „ale”, co nie? W tym przypadku nasze „ale” brzmi: „A co jeżeli stoper, który użyliśmy, podczas włączania nie pokazywał zero, a jakąś inną wartość np. 100 s?” Taka sytuacja powoduje, że nasz świetny algorytm na mierzenie czasu ruchu wcale nie jest taki świetny.
Dlaczego? Bo jeżeli wyłączymy stoper po 20 sekundach, to on wcale nie będzie wskazywał 20 sekund, a 120 sekund, czyli błędny wynik.
Ale Szymon, co to jest za problem?
Skoro na początku było 100 sekund, to po po prostu od 120 sekund odejmij to 100 s i będziemy mieli 20 s, czyli wynik prawidłowy.
Easy peasy lemon squeeze.
I wiesz co? To właśnie jest rozwiązaniem naszego problemu z pomiarem czasu. Nas nie interesuje co dokładnie będzie pokazywał stoper na końcu, a to o ile zmieniła się wartość, którą on wskazuje. W fizyce, żeby zaznaczyć, że interesuje nas o ile coś się zmieniło używamy literki $\Delta$ (jest to grecka duża litera delta). Więc skoro nas interesuje o ile zmienił się czas to po fizycznemu zapiszemy to tak $\Delta t$. Ale to nie koniec naszej dobrej passy w tworzeniu doskonałego algorytmu pomiaru czasu. Aby policzyć prawdziwy czas trwania ruchu zrobiliśmy takie cóś
$\Delta t=120\text{s}-100\text{s}=20\text{s}$
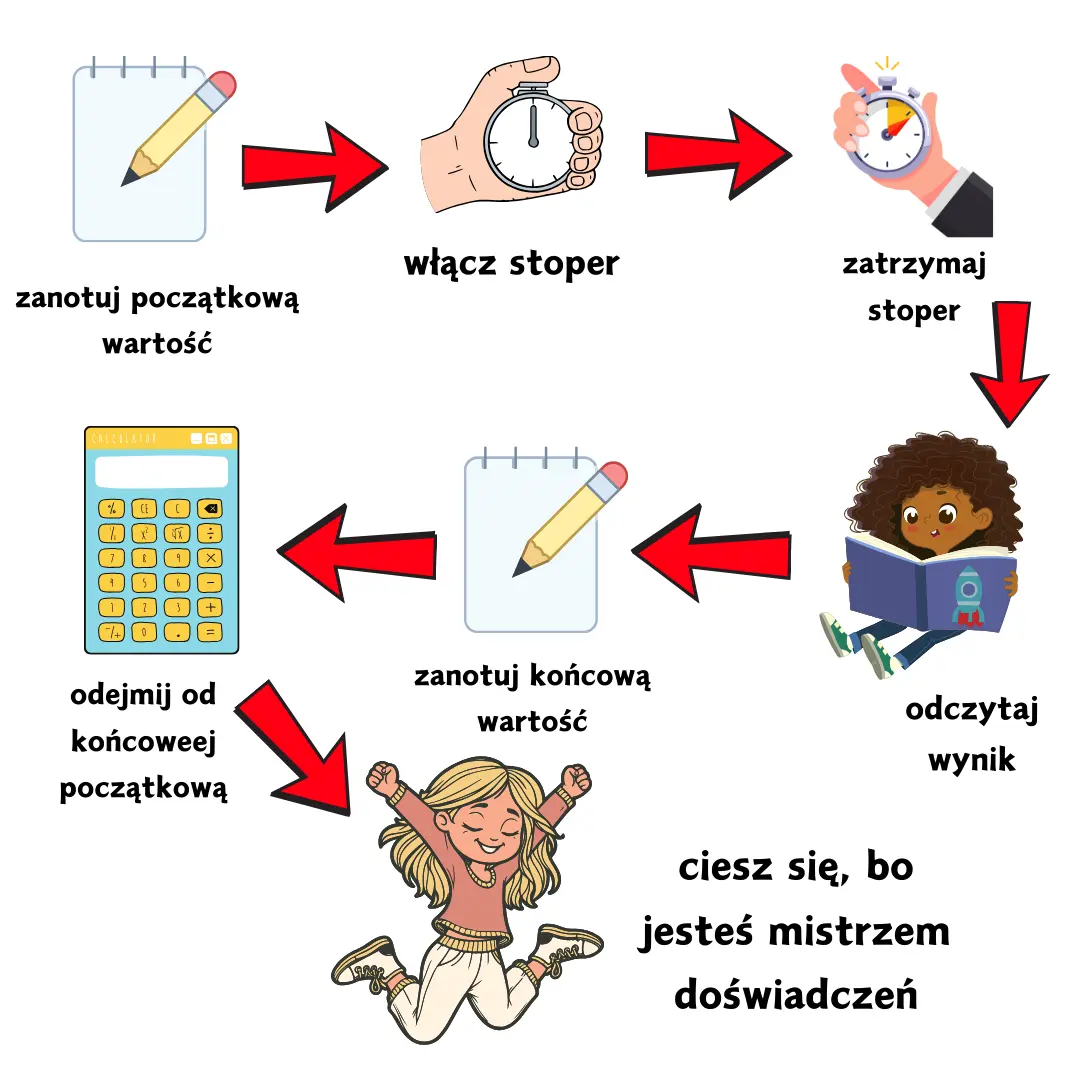
Od wartości którą wskazywał stoper na końcu, odjęliśmy wartość którą wskazywał na początku. Fizyka uwielbia literki, więc dołóżmy je. Niech wartość, którą wskazywał stoper na początku przebierze się za literkę $t_{0}$, a wartość na końcu za literkę $t_{k}$. Wtedy to możemy zapisać
$\Delta t=\underbrace{120\text{s}}_{t_{k}}-\underbrace{100\text{s}}_{t_{0}}=20\text{s}$
$\Delta t=t_{k}-t_{0}$
I właśnie, wspólnymi siłami, stworzyliśmy idealny algorytm mierzenia ile czasu coś trwało. Czujesz to? To zapach zwycięstwa.

Nie samym czasem ruch stoi - szybkość wskakuje na scenę
Z poprzedniej części wiemy już, o ile metrów ciało się przemieściło. Wiemy już też ile czasu mu to zajęło. Nie wiem jak cię, ale mnie teraz korci zapytać:
„To jak szybko się ono ruszało?”

Wyobraźmy sobie, że rower w ciągu 20 sekund przejechał drogę 200 metrów. Oznacza to, że w ciągu każdej sekundy przejeżdżał 10 metrów. Wartość tą mogę zapisać też tak $\frac{10\:\text{metrów}}{1\:\text{sekunda}}$, co w formie skróconej jest równe $\frac{10\:\text{m}}{1\:\text{s}}$ lub $10\frac{\text{m}}{\text{s}}$. To co policzyłem nazywamy szybkością i mówi nam ona o jaki dystans przemieszczamy się w czasie, który jest w mianowniku (pod kreską ułamkową). Literka jaką w fizyce zwykliśmy oznaczać szybkość to $v$. A więc szybkość roweru to $v=10\frac{\text{m}}{\text{s}}$.
A w jaki sposób ja właściwie to policzyłem? Podzieliłem całą drogę przejechaną przez rower (oznaczmy ją jako $s$), czyli 200 metrów, przez czas jaki rower na to potrzebował (oznaczmy jako $\Delta t$), tj. 20 sekund.
$v=\frac{200\:\text{m}}{20\:\text{s}}\xrightarrow[\text{literkach}]{\text{czyli na}}v=\frac{s}{\Delta t}$
Ps. Bardzo często możemy spotkać się ze wzorem
$v=\frac{s}{t}$,
czyli bez użycia znaku $\Delta$. Dlaczego tak? Często przy pomiarze zakłada się, że czas początkowy $t_{0}$ jest równy 0 sekund, czyli tak jak w naszym początku zabawy ze stoperem.
W takim przypadku
$\Delta t = t_{k} – t_{0}= t_{k} – 0\:\text{s} = t_{k}$,
czyli nasza zmiana czasu jest równa czasowi końca pomiarów ($\Delta t=t_{k}$). I dlatego, dla uproszczenia, we wzorach nie zapisujemy wtedy znaku $\Delta$ i odpuszczamy sobie indeks $k$ w $t_{k}$.
To była karta pułapka - z puszczy wyłania się szybkość średnia
Wiemy jak szybko jechał rower, ale… Kurde, znowu to ale! Co tym razem?!

Wyszło, że rower co sekundę przejeżdża 10 metrów i dzięki temu po 10 sekundach jest 200 metrów dalej. A co jeśli rower nie jechał cały czas tak samo? Co jeśli w połowie trasy się wywrócił, a potem przyspieszył, żeby nadrobić czas? Co wtedy?
Wtedy nasze obliczenia tego nie uwzględniły. To co my obliczyliśmy, to szybkość średnia. Czyli jeżeli rower jechał tak samo szybko przez cały czas $\Delta t$ i przejechał drogę $s$ to musiał jechać właśnie z tą szybkością średnią. Ale z wartościami średnimi jest taki problem, że często gubią dużo informacji.

Przykład? Ja jem mięso, a ty kapustę z ryżem. Więc średnio każdy z nas je gołąbki. Widzisz to? Średnio wyszło coś, co w żaden sposób nie pokrywa się z rzeczywistością. I oczywiście jest to przykład bardzo skrajny, ale jednak który może się zdarzyć.
I tego musimy być świadomi przy liczeniu naszej szybkości średniej. Bo może się okazać, że nam wyszło, że rower średnio porusza się szybkością $10\frac{\text{m}}{\text{s}}$, a rower mógł ani razu jechać z tą wartością.
Dlatego, żeby wszystko było jednoznaczne uzupełnijmy nasz symbol szybkości o informacje, że jest ona średnia, a więc zapiszmy ją jako $v_{\acute{s}r}$.
Podsumowując wzór na nią ma postać $v_{\acute{s}r}=\frac{s}{\Delta t}$
Czy tu wszystko jest jasne?
Czas spada na łeb, na szyję - nieodzowny znak, że szybkość chwilowa nadciąga
Jeżeli tak, to możemy sprawy zamienić w jeszcze ciekawsze (serio, da się). Spróbujmy zastanowić się jak możemy dowiedzieć się z jaką konkretną szybkością poruszał się rower (aaa, zapytanie go o to odpada, to od razu zaznaczę, żeby potem nie było). Co rozumiem przez pojęcie konkretnej szybkości w danym momencie? Już tłumaczę. Kojarzysz liczniki rowerowe? One wskazują jak szybko jedziesz, dokładnie w danym momencie, w danej konkretnej chwili. I to co one wskazują jest właśnie pożądaną przeze mnie informacją. A, właśnie, ponieważ jest to szybkość, którą rower ma dokładnie w konkretnej chwili to od tego momentu o tej szybkości będziemy mówić, że jest to szybkość chwilowa. Jest to też oficjalna fizyczna nazwa na takie cóś.

Wracając do liczników rowerowych, to jak one liczą tą szybkość chwilową? Żeby taki licznik działał, montuje się na kole taki specjalny nadajnik, a drugi element (nazwijmy go odbiornikiem) montuje się nieopodal koła. I kiedy koło się kręci to nadajnik mija odbiornik, a odbiornik to rejestruje. Jeden obrót koła, to raz zarejestrowany nadajnik. I potem jak jedziemy na rowerze, to jak wszyscy wiemy – koło się kręci. W rezultacie nadajnik mija odbiornik, a ten liczy. Co liczy? Ile razy np. w ciągu sekundy mija go ten nadajnik. A potem liczbę obrotów zamienia na drogę jaką pokonał rower. Drogę dzieli przez czas i mamy naszą szybkość chwilową.
Chwila, chwila. Szymon, wstrzymaj konie!
Licznik rowerowy dzieli drogę przejechaną przez czas i mówisz, że to jest szybkość chwilowa? Przecież przed chwilą była mowa, że tak się liczy szybkość średnią. To jak to jest? Jaka jest różnica pomiędzy szybkością średnią, a chwilową?
Różnica jest w detalach. Jeżeli przedział czasu jest duży, to rower może w tym czasie często zmieniać szybkość. A jeżeli czas jest króciutki, to szanse na, że w trakcie rower zwalniał bądź przyspieszał są mniejsze. A kiedy szansa jest najmniejsza? Wiemy, że czym krótszy czas, tym mniejsza szansa na zmianę szybkości. Więc może zero sekund? Nie, to nie ma sensu. Przecież skoro ruch trwał 0 sekund, to rower nic nie mógł przejechać. To co jest małą wartością, ale jest większe od zera? Hmmmm…
Możemy powiedzieć, że czas ruchu, czyli nasza $\Delta t$ jest tak mała, że prawie jest równa zero, ale nie jest równa zero. Sprytne, co nie? Jeżeli mówimy o tak małych wartościach, to wtedy używamy takich stwierdzeń, że $\Delta t$ dąży do zera (możemy to zapisać w taki sposób $\Delta t\rightarrow0\text{s})$, albo $\Delta t$ jest infinitezymalnie małe (infinitezymalnie oznacza nieskończenie, a nazwa wzięła się z angielskiego słowa infinity, czyli właśnie nieskończoność)

Podsumowując, jeżeli we wzorze na szybkość średnią, przedział czasu $\Delta t$ skrócimy do absurdalnie małych wartości, to otrzymamy wzór na szybkość chwilową (oznaczaną jako $v_{chw}$) i zapiszemy to tak
$v_{chw}=\left(\frac{s}{\Delta t}\right)_{\Delta t\rightarrow0\text{s}}$
Hello mr prędkość - czyli podobnie, ale inaczej (i to jak inaczej)
Zanim do niego przejdźmy, uzgodnijmy układ odniesienia – dla wektorów jest to bardzo ważne. Załóżmy, że oś pozioma (zwana x-ową) będzie skierowana w prawo, a oś pionowa (zwana y-ową) będzie skierowana do góry. Jak już to zrobiliśmy, to lećmy dalej z tematem.
Załóżmy, że zaobserwowaliśmy, że nasz rower przemieścił się o wektor $\Delta\vec{r}=[200\:\text{m},\: 80\:\text{m]}$, w czasie $\Delta t=10\:\text{s}$. O jaki wektor rower przemieszczał się w ciągu jednej sekundy? Zróbmy podobnie jak wcześniej z szybkością – podzielmy to o ile się przemieścił przez czas jaki mu to zajęło, a więc
$\frac{\Delta\vec{r}}{\Delta t}=\frac{[200\:\text{m},\: 80\:\text{m]}}{10\:\text{s}}$
Kiedy dzielimy wektor przez liczbę, to dzielimy każdą składową przez nią
$\frac{[200\:\text{m}, 80\:\text{m]}}{10\:\text{s}}=\left[\frac{200\:\text{m}}{10\:\text{s}},\frac{80\:\text{m}}{10\:\text{s}}\right]=[20\frac{\text{m}}{\text{s}},8\frac{\text{m}}{\text{s}}]$
A więc możemy zapisać
$\frac{\Delta\vec{r}}{\Delta t}=[20\frac{\text{m}}{\text{s}},8\frac{\text{m}}{\text{s}}]$
Czyli wyszło nam, że w ciągu każdej sekundy nasz rower przemieszczał się o wektor $[20\:\text{m},8\:\text{m}]$. Czyli w naszym układzie odniesienia przemieszcza się o 20 metrów w prawo i 8 metrów w górę.
To co obliczyliśmy dzieląc wektor przemieszczenia $\Delta\vec{r}$, przez czas $\Delta t$ nazywamy prędkością i oznaczamy ją w taki sposób $\vec{v}$
$\underbrace{\vec{v}}_{\text{prędkość}}=\frac{\Delta\vec{r}}{\Delta t}$
Jednostką prędkości są metry na sekundę.
Z tak liczoną prędkością jest jednak jeden mały problem, jedno małe „ale”.

To „ale” brzmi dokładnie takie samo, jak przy szybkości. To co policzyliśmy to średnia prędkość ($|\vec{v}_{\acute{s}r}|$), ponieważ w rozważanym przedziale czasu $\Delta t$, prędkość mogła się zmieniać. A więc, uzupełnijmy nasz wzór o brakujące oznaczenia
$\vec{v}_{\acute{s}r}=\frac{\Delta\vec{r}}{\Delta t}$
Długość wektora prędkości średniej - to się porobiło, dłuższej nazwy się nie dało?
Jak każdy wektor, tak i wektor średniej prędkości ma swoją długość. Długość tą możemy nazwać również wartością prędkości średniej i oznaczyć w taki sposób $|\vec{v}_{\acute{s}r}|$. Aby ją obliczyć postępujemy w sposób typowy dla wektorów (dokładniejszy opis znajdziesz tutaj).

Ale Szymon, czym jest ta długość i czym to się różni od wektora?
Wektor prędkości średniej $\vec{v}_{\acute{s}r}$ informuje nas w jaki sposób się coś porusza (w naszym przypadku rower porusza się w stronę prawego górnego rogu) i jak szybko w każdą stronę (20 metrów na sekundę w prawo i 8 metrów na sekundę w górę). Zaś wartość prędkości średniej $|\vec{v}_{\acute{s}r}|$ totalnie ignoruje kierunek ruchu i mówi nam jak szybko przemieszało się ciało. Mam nadzieję, że teraz różnica między tymi dwoma pojęciami jest teraz dla ciebie jasna.
Ale jaka jest wartość twoja prędkość TERAZ? - prędkość chwilowa pędzi na ratunek
Wiemy, że długi czas pomiaru wiąże się z ryzykiem, że rower zmieniał prędkość. I naszym sprytnym rozwiązaniem przy szybkości $v$ było skrócić czas pomiaru, żeby nie dać szans rowerowi na takie niecne działania. Ta strategia zadziała też przy prędkości. A więc proszę państwa, oto przed państwem, jedyny w swej postaci, wzór na wektor prędkości chwilowej $\vec{v}_{chw}$
$\vec{v}_{chw}=\left(\frac{\vec{r}}{\Delta t}\right)_{\Delta t\rightarrow0\:\text{s}}$

Długość wektora prędkości chwilowej - kolejna długa nazwa, ach ta fizyka
Co tu dużo mówić. Nasz wektor prędkości chwilowej $\vec{v}_{chw}$ jest wektorem, więc ma swoją długość, którą my możemy nazywać wartością prędkości chwilowej i oznaczać jako $|\vec{v}_{chw}|$. Wartość tą liczymy tak samo jak długość dowolnego innego wektora (więcej tutaj). A jeżeli zastanawiasz się jaka jest różnica między wartością prędkości chwilowej $\vec{v}_{chw}$, a wartością tego wektora $|\vec{v}_{chw}|$, to spójrz dwie sekcje wyżej na różnice między wektorem prędkości średniej $\vec{v}_{\acute{s}r}$, a wartością prędkości średniej $|\vec{v}_{\acute{s}r}|$. Różnice te są identyczne dla prędkości chwilowej $\vec{v}_{chw}$.

Różne gwary fizyczne - wartość prędkości średniej, a średnia wartość prędkości
W różnych miejscach, te same rzeczy są różnie nazywane. Jest to dla nas oczywiste. W Polsce na kota, mówimy kot, ale w takiej Anglii wołają cat. No ale są to różne języki, więc jasna sprawa, że tak jest. Niestety w fizyce też czasem się zdarza, że niektóre elementy mają różne nazwy, w zależności od tego kto mówi. I tak, w niektórych książkach można spotkać, że to co my nazywamy szybkością średnią $v_{\acute{s}r}$, ktoś inny nazwał średnią wartością prędkości.

I tutaj trzeba być ostrożnym, bo my już wprowadziliśmy coś bardzo podobnie brzmiącego, a mianowicie wartość prędkości średniej $|\vec{v}_{\acute{s}r}|$. My już wiemy, że szybkość średnia, to nie to samo co wartość prędkości średniej, co możemy jeszcze zapisać tak
$v_{\acute{s}r}\neq|\vec{v}_{\acute{s}r}|$
a więc również i
średnia wartość prędkości $\neq$ wartość prędkości średniej
No, i teraz, nawet jak spotkasz kogoś obco-fizyczno gadającego będzie wiadome, co mówi xD
A co do mnie, w dalszej części mojej pisaniny na tej stronie, będę używał tylko tych stwierdzeń, które wspólnie wprowadziliśmy. Czyli bez żadnych średnich wartości prędkości.
I to by było dziś na tyle. Niech kinematyka będzie z tobą i pamiętaj, unikaj zjeżdżalnio tarek
A jeżeli jesteś odważny, to spróbuj sił w quizie poniżej.

