Słownik fizyka
D
- Długość wektora – jeżeli wektor narysowalibyśmy jako strzałka, to mierząc jej długość magiczną linijką, mierzymy długość wektora. Ale czym jest magiczna linijka? To taki gadżet, który przed chwilą wymyśliłem, który liczy długość strzałki w centymetrach (czyli tak normalnie), a potem wynik zamienia na jednostki odpowiadające wektorowi.
Przykład. Mamy wektor siły. Mierzymy długość i wychodzi 5 cm. Linijka wie, że 1 cm wektora siły to 30 N, więc wektor 5-centymetrowy to 5*30N, czyli 150 N i to jest długość naszego wektora. Ponieważ magiczne linijki nie istnieją, to często naszym zadaniem jest znalezienie tego przelicznika 1 cm na inne jednostki. No cóż, lajf is brutal.
Jeżeli nasz wektor to $\vec{a}$, to długość tego wektora najczęściej oznaczamy tak $|\vec{a}|$
- Droga – określa jaki dystans ktoś przeszedł/przejechał/przeleciał itd. Co ciekawe, nawet jeżeli będziesz szedł do tyłu, to droga będzie rosła. Najłatwiej wyobrazić sobie tutaj krokomierz, który masz w telefonie. Jakbyś nie szedł, nie zmniejszysz liczby kroków, które zrobiłeś danego dnia – ta liczba może tylko się nie zmieniać, bądź rosnąć. W fizyce mówi się też, że droga to długość toru ruchu. Drogę najczęściej oznaczamy symbolem $s$
Słownik fizyka powstał dlatego, że niektóre słowa używane potocznie nie oznaczają tego samego co w fizyce. Innych słów po prostu nie używamy na co dzień. Dlatego zbieram tu słowa, które często są problematyczne w rozumieniu fizycznego żargonu. A następnie tłumaczę tak by było to zrozumiałe, czyli totalnie nie podręcznikowo xD
Aby ułatwić korzystanie, poniżej znajdziesz wypisane literki, które od razu pozwolą przeskoczyć ci do odpowiedniej sekcji. Udanego korzystania 😀
K
- Kierunek wektora – wyobraź sobie wektor jako strzałkę. Jeżeli weźmiesz teraz linijkę i ołówek, to możesz przedłużyć tę strzałkę, tak by postała prosta. Udało się? Gratulacje, właśnie stworzyłeś kierunek wektora, czyli prostą, na której on leży
P
- Położenie – patrz wektor położenia
- Prędkość – wektor mówiący o tym o jaki wektor przemieszczenia przesunie się ciało w ciągu jednostki czasu. Przykład. Wektor prędkości $[8, 5]\frac{\text{km}}{\text{h}}$ informuje nas, że ciało po 1 godzinie przemieści się o 8 km zgodnie z osią x (czyli najczęściej w prawo) i 5 km zgodnie z osią y (najczęściej w górę). Najczęściej prędkośc oznaczamy symbolem $\vec{v}$. Dokładniejsze wprowadzenie do prędkości znajdziesz tutaj
- Prędkość średnia – ciało przemieszczając się z jakiegoś położenia początkowego do końcowego może jechać z różnymi prędkościami. Istnieje jednak pewna prędkość, z którą ciało mogłoby cały czas jechać i pokonałoby ono cały dystans w tym samym czasie, co w momencie, gdy zmieniało prędkości. Taka prędkość, to właśnie prędkość średnia. Najczęściej oznaczana jest ona symbolem $\vec{v}_{śr}$. Dokładniejsze wytłumaczenie, wraz ze wzorami znajdziesz tutaj
- Przemieszczenie – wektor mówiący w jaki sposób przemieściło się ciało, a który liczy się odejmując współrzędne końcowe ciała od początkowych. Nie uwzględnia ono jednak toru ruchu ciała – czyli w jaki sposób ciało dostało się z miejsca początkowego do końcowego. Wektor przemieszczenia najczęściej oznaczany jest symbolem $\Delta\vec{r}$. Więcej o wektorze przemieszczenia znajdziesz tutaj
- Przyspieszenie – wektor mówiący jak w czasie zmienia się wektor prędkości. Mówiąc po ludzku, jeżeli ciało ma przyspieszenie, to albo zwalnia, albo skręca, albo przyspiesza. Istnieją tez opcje łączone: zwalnia i skręca, bądź przyspiesza i skręca. Dokładne wytłumaczenie przyspieszenia znajdziesz tutaj Przyspieszenie najczęściej oznaczane jest symbolem $\vec{a}$
- Punkt materialny – to ciało które ma masę, a którego rozmiary totalnie olewamy. Czyli np. jeżeli założymy, że słoń jest punktem materialnym, to tak naprawdę w naszej głowie będziemy mieli obraz słonia ściśniętego do rozmiarów ziarenka piasku, albo jeszcze bardziej. Ale nadal ten ściśnięty słoń będzie ważyć tyle samo. (ps. w tym eksperymencie myślowym nie ucierpiało żadne zwierzę)
- Punkt odniesienia – w układzie współrzędnych jest to najczęściej punkt (0,0). A tłumacząc po normalnemu, punkt odniesienia to dla nas taki punkt orientacyjny, względem którego mówimy o położeniu rzeczy lub ich ruchu. Dokładniejsze wytłumaczenie znajdziesz tu
- Punkt zaczepienia wektora – krótko mówiąc, miejsce, gdzie wektor ma swój początek, czyli tą część bez strzałki
R
- Ruch prostoliniowy – ciało porusza się wzdłuż linii prostej. Nie ma znaczenia czy do przodu, czy do tyłu. Ważne, że nie skręca. Więcej o rodzajach ruchu znajdziesz tu
- Ruch krzywoliniowy – jeżeli ciało nie jedzie po idealnej linii prostej, to mamy do czynienia z ruchem krzywoliniowym. Więcej o rodzajach ruchu znajdziesz tu
- Ruch jednostajny – ciało jedzie cały czas z dokładnie tą samą szybkością. Więcej o rodzajach ruchu znajdziesz tu
- Ruch jednostajny prostoliniowy – ciało jedzie cały czas z dokładnie tą samą szybkością i cały czas porusza się wzdłuż jednej prostej. Więcej o rodzajach ruchu znajdziesz tu. A dokładniejszy opis dokładnie tego typu ruchu znajdziesz tutaj
- Ruch jednostajnie przyspieszony – ciało co sekundę przyspiesza o dokładnie tyle samo. Więcej o rodzajach ruchu znajdziesz tu
- Ruch jednostajnie opóźniony – ciało co sekundę zwalnia o dokładnie tyle samo. Więcej o rodzajach ruchu znajdziesz tu
- Ruch jednostajnie zmienny – ciało co sekundę zmienia szybkość o dokładnie tyle samo. Ze względu na to, czy zmiany te zmniejszają szybkość, czy zwiększają ten ruch możemy podzielić kolejno na ruch jednostajnie opóźniony i jednostajnie przyspieszony. Więcej o rodzajach ruchu znajdziesz tu
S
- Skalar – fancy fizyczna nazwa na liczbę taką jak np. 8, czy $-\sqrt{2}$. Więc jeśli widzisz gdzieś np. takie zdanie „Masa jest skalarem”, to równie dobrze możesz to sobie w głowie przeczytać jako „Masa jest liczbą”.
- Składowa wektora – jeżeli zapiszemy wektor przy pomocy nawiasu, to składowa to liczba oddzielona od innych przy pomocy przecinka. Weźmy wektor [3, -5]. Składowymi tego wektora jest 3 oraz -5. Proste co nie? A jeśli ciekawi cię po co one są, to najlepiej zrozumiesz to na przykładzie.
- Szybkość – wielkość liczbowa określająca jaką drogę ciało jest w stanie pokonać w jednostce czasu. Przykład. Szybkość $5\frac{\text{km}}{\text{h}}$ oznacza, że ciało w ciągu godziny jest w stanie przejechać 5 km. Najczęściej szybkość oznacza się symbolem $v$. Dokładniejsze wytłumaczenie szybkości znajdziesz tutaj
- Szybkość średnia – wyobraź sobie, że jedziesz samochodem z Gdańska do Warszawy. Dużą część drogi pokonałeś szybko na autostradzie, ale część wlokłeś się w korkach. Była też jedna przerwa na siku. Wyraźnie widać, że podczas jazdy jechałeś raz szybciej, a raz wolniej. Ale możemy wyobrazić sobie, że mógłbyś jechać całą trasę z tą samą szybkością non stop i poświęcić na to tyle samo czasu ile w opcji z przerwami i autostradami. Ta wyobrażona sobie przez nas szybkość to właśnie szybkość średnia. Najczęściej szybkość średnią oznacza się symbolem $v_{śr}$. Dokładniejsze wytłumaczenie szybkości średniej znajdziesz tutaj
T
- Tor ruchu – dokładny kształt trasy którą coś się poruszało. Przykład. Wyobraź sobie, że chodzisz po domu w zabłoconych butach. Chwilę później do domu przychodzi twoja mama. Ślady, które zostawiłeś łatwo pozwolą jej domyślić się jak szedłeś. A więc te ślady błota są twoim torem ruchu.
U
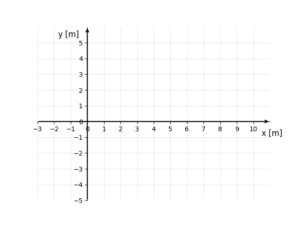
- Układ współrzędnych – najczęściej układ współrzędnych to dwie prostopadłe do siebie strzałki, nazywane osiami i wygląda jak na rysunku poniżej. Służy on do określania położeń jakiś ciał. Więcej o tym znajdziesz tutaj
W
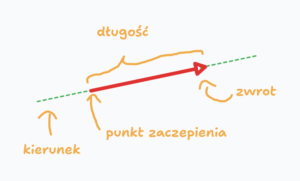
- Wektor – twór matematyczny, który rozpoznajemy po tym, że nad literką jest strzałka. Przykłady wektorów wyglądają tak: $\vec{a}$, $\vec{F}$, $\vec{p}$. Wektory możemy narysować jako strzałka (albo używając żargonu matematycznego – odcinek skierowany). Ta strzałka ma 4 ważne cechy, które ją opisują i są to: długość, zwrot, kierunek i punkt zaczepienia. Ale wektor można opisać też bez rysowania strzałek. Wtedy używamy nawiasów kwadratowych, w które wpisujemy liczby oddzielone przecinkami. Wygląda to na przykład tak [2, -5]. Każda liczba w wektorze to tak zwana składowa. Najlepiej złapiesz, o co biega na przykładzie, więcej wpadaj tutaj. Tłumaczę tam wektor przemieszczenia, ale wektor to wektor. Jak złapiesz idee, to będziesz ogarniał wszystkie wektory 😀
- Wektor położenia – wektor dający nam informację, gdzie znajduje się w chwili obecnej jakieś ciało. Ma on też informacje o tym, jak dojść do tego ciała od punktu odniesienia. Najczęściej wektor położenia oznacza się symbolem $\vec{r}$. Więcej o tym wektorze znajdziesz tutaj
Z
- Zwrot wektora – informacja z której strony wektor ma narysowaną strzałkę. Jeżeli mówimy, że wektory mają taki sam kierunek, ale przeciwne zwroty, to znaczy, że te wektory są do siebie równoległe, ale mają strzałki w przeciwne strony
