Przemieszczenie i droga - teoria
Spis treści – czyli co tutaj znajdziesz:
(przydatne info – jak klikniesz któryś zielony napis poniżej, to od razu cię tam przeniesie)
Układ współrzędnych - po co to?
Każda historia potrzebuje jakiegoś świata, w którym może rozgrywać się fabuła. Nie inaczej jest z fizyką, w której takim światem jest układ współrzędnych. Układy współrzędnych mogą być różne, ale najczęściej spotykanym jest taki jak na rysunku poniżej, czyli składający się z dwóch prostopadłych strzałek, nazywanych osiami. Przy strzałkach widzimy napisy „x [m]” oraz ,,y [m]”. To co nie jest w nawiasie jest nazwą osi (takim jakby jej imieniem), a w nawiasie kwadratowym są jednostki w jakich są podane wartości na osiach.
Układ taki umożliwia opisywanie ruchu w dwóch wymiarach (góra-dół, prawo-lewo), czyli dokładnie tak jak na mapach.
Punkt odniesienia - przyzywam cię!
Skoro już mowa o mapach, to jak się z nich korzysta? Wyjmujemy ją i próbujemy się zorientować gdzie na niej jesteśmy, albo gdzie jest to czego szukamy. W tym celu szukamy punktów charakterystycznych, którymi może być znany nam sklep, jakaś miejscowość lub wielki znacznik „Tu jesteś”. Każda z tych rzeczy to dla nas punkt odniesienia.
Używamy tego non stop. Przykład? Jak będziesz koło warzywniaka, skręć w prawo. Tutaj punktem odniesienia jest warzywniak.

A skoro już złapaliśmy jak to działa, w naszej codzienności, to pojawia się pytanie: „A jak to będzie w fizyce?”. Już odpowiadam. W fizyce też mamy punkt odniesienia i może nim być cokolwiek, czyli tak jak w życiu. Jedyna różnica jest taka, że w fizyce punkt odniesienia znajdować się będzie w punkcie (0,0) układu współrzędnych, czyli tam, gdzie nasze osie się przecinają.
Punkt materialny - czyli dieta (prawie) cud
Mamy już zbudowany świat i zdecydowaliśmy co będzie pępkiem tego świata (czyli wybraliśmy punkt odniesienia). A skoro tworzymy historię, to fajnie dodać bohaterów do świata, bo bez tego to raczej nudno może być (nie znam się aż tak, ale nigdy nie czytałem książki, w której nie było bohaterów. Przypadek? Nie sądzę).

Więc umieśćmy w naszym układzie kogoś epickiego.
Kogoś takiego jak Pan P.
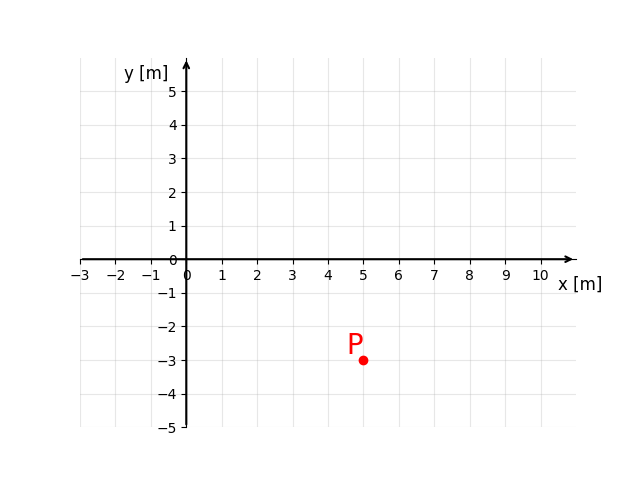
Wypadło na to, że pan P, zrespił się na współrzędnych (5, -3), czyli 5 metrów na prawo od układu odniesienia i 3 metry w dół od niego. Ale zaraz, zaraz. mówiąc, że jest on na tych współrzędnych, co mamy na myśli? To są współrzędne jego głowy, prawej nogi, czy wątroby? Człowiek ma jakąś szerokość, więc prawa ręka będzie gdzie indziej niż lewa ręka. Czy musimy dawać współrzędne każdego punktu ciała? Przecież to by było mega niepraktyczne. Jak udostępniamy komuś swoją lokalizację w telefonie, to udostępniamy jedne współrzędne, a nie milion.

I wtedy jak rycerz na białym koniu, przybywa punkt materialny z pieśnią nadziei na ustach. A pieśń ta brzmi:
,,Nie lękajcie się, olejcie rozmiary ciała"
I my w kinematyce korzystamy z tych mądrych słów i olewamy rozmiary pana P. Mówimy: ,,on jest tam” i podajemy współrzędne. W rezultacie wszyscy są zadowoleni i żyją długo i szczęśliwie.
Dokładnie tak samo jest jak udostępniamy swoją lokalizację, albo gdy szukamy czegoś na google maps. Ci to dopiero są mocni – cały budynek zwijają do jednej współrzędnej, czyli do jednego punktu.
No i koks. Mamy to, ale tak dla ścisłości, co pod względem fizycznym oznacza, że zamieniliśmy kogoś w punkt materialny? Odpowiedź na to jest prosta. Zamieniliśmy kogoś w punkt, czyli coś co nie ma rozmiaru, ale o czym dowiemy się w kolejnych działach (spoiler alert!), jego masa pozostaje bez zmian. Ale to na spokojnie, masa nam teraz nie potrzebna. Najważniejsze, że wiemy, gdzie jest Pan P (pamiętamy, współrzędne (5,-3)).
Wektor położenia - nasz nowy funfel?
Czy to nam wystarczy? A czy Frodo we „Władcy Pierścienia” wystarczyło wiedzieć, gdzie jest Mordor? Nie, musiał jeszcze wiedzieć jak tam dojść. Czyli potrzebował wskazówek jak iść.

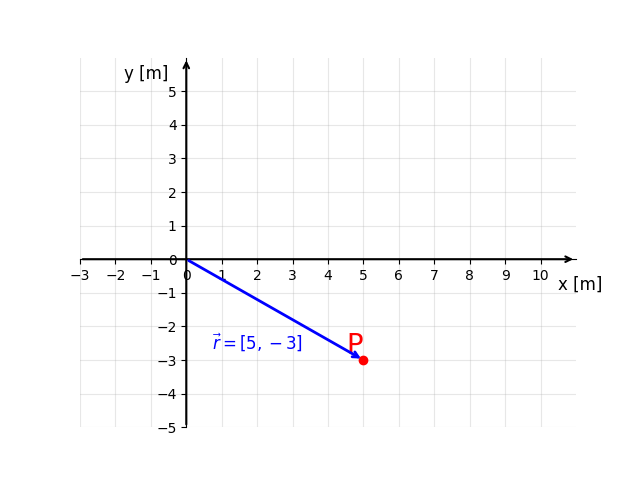
W kinematyce taką wskazówką są wektory. A wektor mówiący jak się gdzieś dostać z punktu odniesienia jest tak specjalny, że ma nawet swoją nazwę – wektor położenia (nazwa intuicyjna, bo mówi nam, gdzie coś się znajduje). Oznaczamy, go jako $\vec{r}$, a jego jednostką są metry. Ponieważ jest to wektor, to możemy zapisać go tak
$\vec{r}=[r_{x},r_{y}]$,
gdzie $r_{x}$ to składowa x-owa naszego wektora, a $r_{y}$ jest składowa y-ową.
Czym to w ogóle jest? Tak jak mówiłem, to są wskazówki jak iść. Składowa $r_{x}$ mówi nam ile metrów od punktu odniesienia trzeba iść zgodnie z poziomą osią (osią x), czyli u nas w prawo by dojść do miejsca, które nas interesuje, a $r_{y}$ ile w kierunku osi pionowej (osi y) w górę. A więc skoro Pan P jest w miejscu (5, -3), to łatwo stwierdzić, że od punktu odniesienia trzeba iść 5 metrów w prawo, czyli $r_{x}=5$. Zaś w pionie trzeba przejść 3 metry w dół. Ponieważ $r_{y}$ mówi o ruchu do góry, to powiemy, że idziemy do góry o -3 metry (to takie dziwne powiedzenie, że idziemy w dół xD), z czego wynika $r_{y}=-3$. Podsumowując $\vec{r}=[5,-3]$.
Zauważyłeś, że jedyna różnica między współrzędnymi Pana P, czyli (5,-3), a wektorem jego położenia, to inne nawiasy? To nie przypadek. Wektor położenia zawsze będzie tak się zachowywał. A dlaczego wektor ma inne nawiasy? Żeby było wyraźnie widać, że to wektor xD
Wektor przemieszczenia - kolejny wektor wkracza na arenę
Świat w którym jest tylko Pan P, a nie ma niczego więcej, jest nudny (nic osobistego Panie P). Dodajmy więc trochę elementów do świata, np. miasto o wdzięcznej nazwie K. W odróżnieniu od rzeczywistości, w pisaniu łatwo stworzyć miasto. Wystarczy, że powiem, że jest na współrzędnych (7,4) i ono się tam pojawia.

A jak to miasto będzie wyglądać na naszej mapie? A no właśnie tak jak tu poniżej widać.
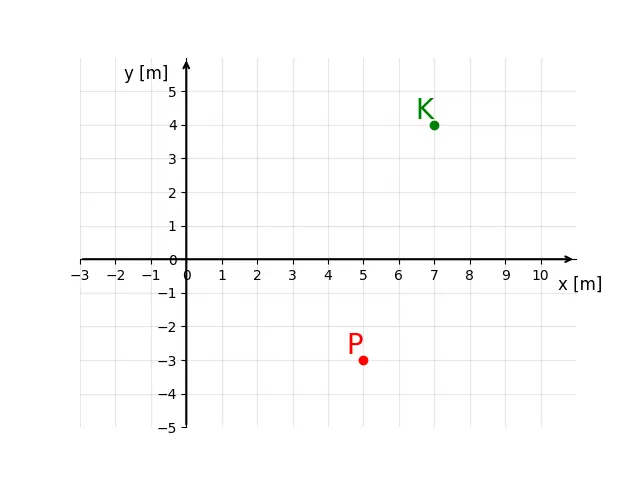
Miasto K, jak już wiesz też ma swój wektor położenia i jest to $\vec{r}_{K}=[7,5]$ (Dodałem dolny indeks K, dla podkreślenia, że chodzi o miasto K). Więc mając już ten wektor łatwo możemy dojść od punktu odniesienia do miasta. Ale, jak zawsze pojawia się jakieś ale, w jaki sposób Pan P ma się dostać do tego miasta? Bez sensu żeby szedł najpierw do punktu (0,0), a dopiero stamtąd do miasta. Istnieje krótsza droga, pokazana na rysunku niżej
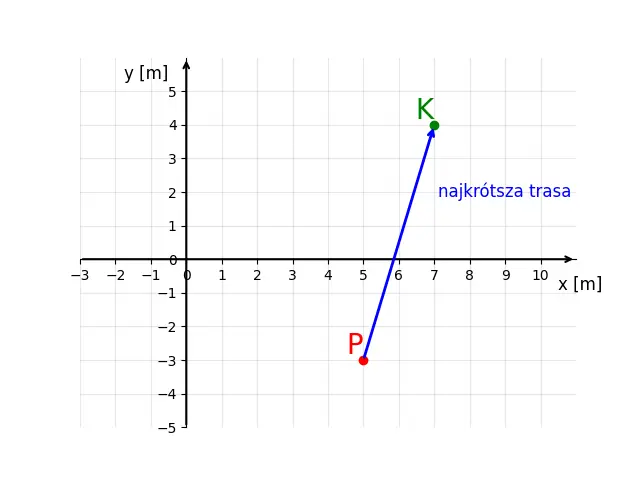
Jak widzisz, trasę tą stworzyłem przy pomocy wektora, czyli odcinka, ze strzałką. Zaczyna się on przy Panu P, a kończy w mieście K. Wektor ten mówi nam jak w sposób najkrótszy dostać się z miejsca startowego do końcowego i nazywa się on wektorem przemieszczenia. Zapisać go możemy na dwa sposoby albo jako $\Delta\vec{r}$, albo $\vec{x}$ (tutaj będziemy używać tego pierwszego sposobu).
A jak się go liczy? Spójrzmy jeszcze raz na zapis tego wektora, $\Delta\vec{r}$. Przed $\vec{r}$ znajduje się symbol $\Delta$ (grecka duża litera delta), która w fizyce często symbolizuje zmianę. Zmianę czego? Tego co znajduje się po niej, czyli u nas zmianę wektora położenia. I z deltą zawsze jest tak, że liczymy ją jako wartość końcowa minus wartość początkowa.
Czyli u nas od wektora położenia końcowego (czyli wektor położenia miasta K) $\vec{r}_{K}$ odejmiemy wektor położenia początkowy (u nas wektor położenia Pana P) $\vec{r}_{P}$
$\Delta\vec{r}=\vec{r}_{K}-\vec{r}_{P}=[7,4]-[5,-3]$
Kiedy odejmujemy wektory, to od współrzędnych pierwszych odejmujemy współrzędne pierwsze, a od drugich drugie. Wygląda to tak
$\Delta\vec{r}=[7,4]-[5,-3]=$
$=[7-5,4-(-3)]=[2,7]$
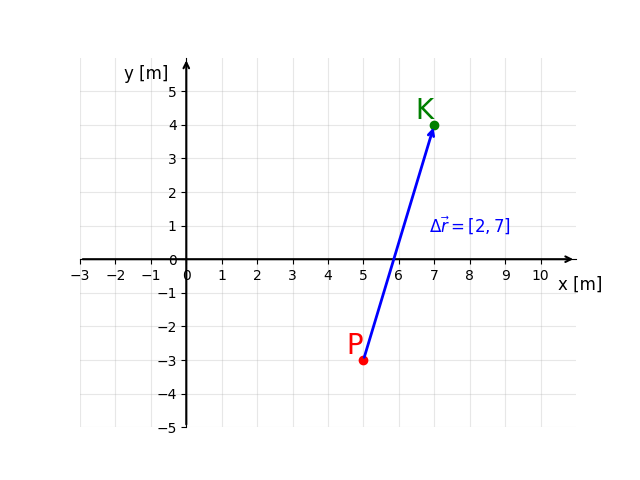
Wyszło nam, że Pan P, musi przejść wektor $\Delta\vec{r}=[2,7]$, czyli musi pójść 2 metry w prawo i 7 metrów w górę i wtedy dojdzie do miasta K. Możemy łatwo sami sprawdzić, czy tak rzeczywiście jest, korzystając z wykresu i licząc kratki
Długość wektora przemieszczenia - czyli ,,daleko jeszcze"?
Wiemy już, jak powinien iść Pan P, ale nie oszukujmy się. On nie będzie szedł najpierw 2 kroki w prawo, a potem 7 w górę. Pójdzie po skosie, żeby nie iść dokoła. To ile metrów przejdzie, zanim dojdzie do miasta K? Dobrze, że pytasz, bo to pozwala nam wprowadzić tak zwaną długość wektora przemieszczenia oznaczaną tak $|\Delta\vec{r}|$ i w skrócie mówi nam ona jak długi jest wektor $\Delta\vec{r}$. Aby policzyć tą długość musimy zaprosić starego greka o imieniu Pitagoras i jego słynny trójkąt prostokątny. Zobacz, że nasz wektor przemieszczenia możemy otoczyć takimi kreskami

A ponieważ mamy tu trójkąt prostokątny, to mogę napisać, że
$(|\Delta\vec{r}|)^{2}=2^{2}+7^{2}$
Czyli po spierwiastkowaniu dwóch stron
$|\Delta\vec{r}|=\sqrt{2^{2}+7^{2}}=\sqrt{4+49}=\sqrt{53}$
Nasz Pan P przeszedł $\sqrt{53}$ metry. Jaki z tego wniosek? Że liczenie długości wektora jest proste. Podnosimy do kwadratu każdą jego składową. Potem to wszystko dodajemy, a na końcu pierwiastkujemy.
Tor ruchu i droga - inna perspektywa
Jak wiemy z własnego życia, nie zawsze idziemy gdzieś po najkrótszej drodze (super dowodem jest chodzenie po sklepie, kto choć raz nie nadłożył tam drogi). Więc Pan P, również mógł nie iść po najkrótszej drodze do miasta K, a po jakieś innej. Specjalnie dla ciebie, skopiowałem trzykrotnie wszechświat Pana P i w każdym z nich ubrudziłem jego buty farbą, tak, by było widać ślady jak szedł. Po nałożeniu trzech zestawów śladów na jeden układ dostaliśmy coś takiego
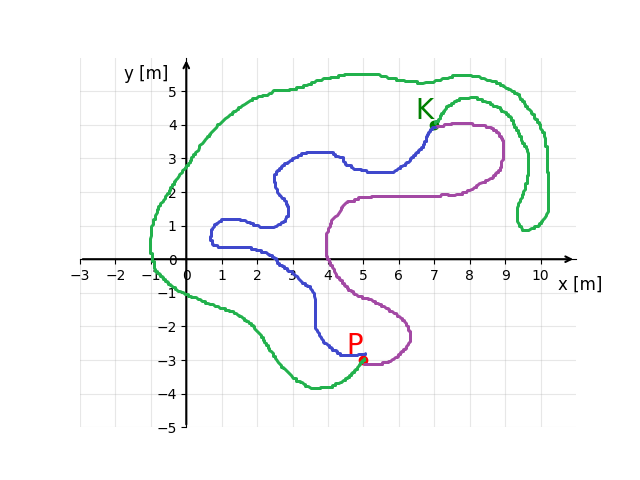
Widzimy, że sposoby w jaki szedł Pan P, są bardzo różnorakie.

Kiedy mówimy o kształtach trasy, to formalnie możemy powiedzieć, że mówimy o torze ruchu (używając tej nazwy, będziesz brzmieć mądrzej i będziesz miał plusy u fizyków).
Co wydaje się oczywiste, w zależności jak wyglądała nasza trasa (czyli jaki był tor ruchu) mogliśmy przejść więcej, albo mniej. Długość toru ruchu ma swoją nazwę, która jest nam bardzo bliska. Domyślasz się? Tak, to droga i oznaczamy ją literką $s$ i liczymy ją w metrach.
Droga, a długość wektora przemieszczenia - częsta karta pułapka
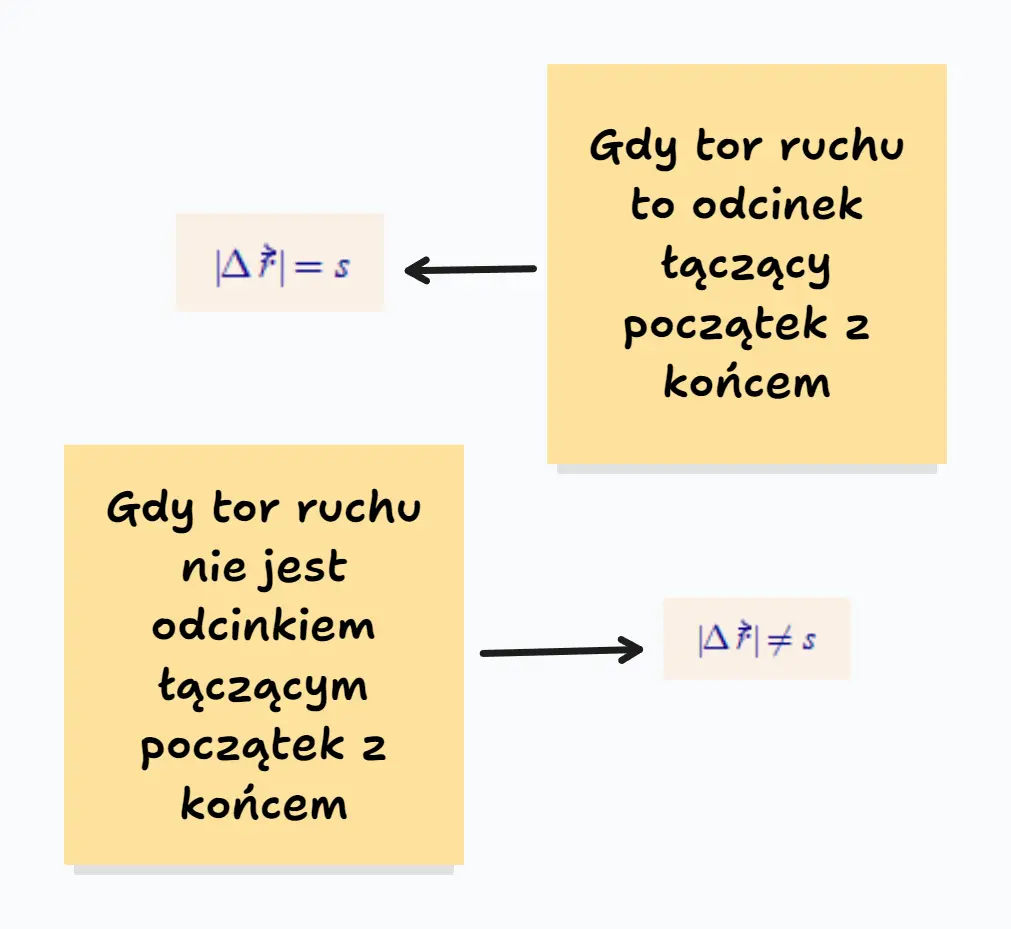
Jak już zobaczyliśmy, wektor przemieszczenia opisuje najkrótszy sposób przejścia od początku do końca. Czyli odpowiada mu tor ruchu będący linią prostą łączącą dwa punkty. I jeżeli analizowany tor ruchu jest taką prostą to droga jest równa długości wektora przemieszczenia, a jeżeli tor nie jest taką prostą, to jedno nie równa się drugiemu. Przedstawiłem to elegancko na rysunku niżej, więc rzuć tam okiem (no dobra, może nie, aż tak elegancko, jak mogło by być, ale na pewno jako tako).
I to by było dziś na tyle. Niech kinematyka będzie z tobą i pamiętaj, unikaj zjeżdżalnio tarek.
A jeżeli jesteś odważny, to spróbuj sił w quizie poniżej.

A jeżeli chcesz od razu wskoczyć do playlisty na YouTubie na której rozwiązuje zadania z tego tematu to klikaj tutaj.
