Czym jest przyspieszenie? - teoria
Spis treści – czyli co tutaj znajdziesz:
(przydatne info – jak klikniesz któryś zielony napis poniżej, to od razu cię tam przeniesie)
Wprowadzenie - jak zacząć historię o przyspieszeniu?
Jeżeli żyjesz na tym świecie dłużej niż 10 minut, zapewne wiesz, że rzeczy mogą się ruszać. Ba, nie tylko mogą się ruszać, ale mogą to robić szybko, wolno, albo jak tylko im się podoba (więcej o tym jak to opisywać, czyli o szybkości i prędkości znajdziesz tutaj).

Jednak jesteśmy też świadomi, że coś co się ruszało nagle może przestać (dramat człowieka, kiedy zjeżdża na sankach i górka się skończyła), albo w drugą stronę, nieruchomy cosiek może zacząć się ruszać (ulubiona szklanka mamy szturchnięta łokciem ze stołu leci na spotkanie ziemi).
Świat jest pełen niespodzianek, ale na szczęście fizyka jest gotowa, żeby radzić sobie i z takimi wyzwaniami. Jeżeli nie wierzysz, to spójrz na sytuację, który kiedyś z nią miałem:
- Oh nie, mój rower zmienił swoją prędkość - powiedziałem spanikowany - Co teraz?! Czy to znaczy, że koniec świata jest coraz bliżej?
- Nie martw się - odpowiedziała spokojnym głosem Fizyka, zaczynając jednocześnie grzebać w kieszeni - właśnie na taką sytuację mam to
Z tymi słowami wyciągnęła z kieszeni niewielki posążek w kształcie małej litery $\vec{a}$, a następnie podstawiła mi go przed oczy
- To mój drogi Szymonie, to jest przyspieszenie. Oznaczamy je literką "a" od angielskiego słowa acceleration, co znaczy właśnie przyspieszenie. Służy ono do...
I zaczęła mi tłumaczyć potęgę przyspieszenia. I nie powiem, coś w tym było, bo mój świat dalej istnieje. Więc jak mogę nie wierzyć w tę potęgę. Nie kojarzę jednak dokładnych słów Fizyki, które później mi powiedziała, więc niestety muszę opowiedzieć ci o przyspieszeniu we własnych słowach. Wiem, że to duża strata, ale chyba damy sobie rade we dwójkę, co nie?
Czym jest przyspieszenie? - ogarnianie na chłopski rozum
Sytuacja, którą przeżyłem z Fizyką dotyczyła zmiany prędkości mojego roweru. Co to znaczy? To znaczy, że na początku mój kochany jednośladowiec jechał z pewną prędkością – nazwijmy ją sobie prędkością początkową i oznaczmy jako $\vec{v}_{0}$, ale po pewnym czasie jego prędkość była inna. Tą drugą prędkość możemy nazwać prędkością końcową i oznaczyć eleganckim znaczkiem $\vec{v}_{k}$. Zauważ, że w poprzednich zdaniach niepostrzeżenie wrzuciłem stwierdzenie, że zmiana ta nastąpiła po pewnym czasie. Ostatnio rozkminiliśmy, że jeżeli mowa o czasie który minął od jednej chwili do drugiej, to oznaczamy to symbolem $\Delta t$.
Wiesz co? Mamy już wszystkich bohaterów naszej historii o przyspieszeniu. Czy to nie ekscytujące? Teraz zostało nam tylko ich odpowiednie zeswatanie.

Jak? No, tu musimy pomyśleć. A wiem, że łatwiej myśli się, kiedy pracuje się na konkretnych wartościach, aniżeli na ogólnych symbolach. Dlatego uznajmy, że mój rower jechał po prostej trasie, bez zakrętów (dzięki temu nie musimy przejmować się wektorami). I załóżmy, że w ciągu 10 sekund przyspieszył od $5\frac{\text{m}}{\text{s}}$ do $15\frac{\text{m}}{\text{s}}$.
O ile przyspieszył mój rower? Musimy tutaj odjąć wartość końcową od początkowej
$10\frac{\text{m}}{\text{s}}=15\frac{\text{m}}{\text{s}}-5\frac{\text{m}}{\text{s}}$
Rower przyspieszył o $10\frac{\text{m}}{\text{s}}$. Super, ale po co nam był w tym wszystkim czas ile mu to zajęło? Ha, bo teraz mogę policzyć o ile przyspieszał w ciągu 1 sekundy. A zrobię to dzieląc wartość o jaką przyspieszył przez czas, jak długo mu to zajęło
$\frac{10\frac{\text{m}}{\text{s}}}{10\text{s}}=1\frac{\frac{\text{m}}{\text{s}}}{\text{s}}=1\frac{\text{m}}{\text{s}}:\text{s}=1\frac{\text{m}}{\text{s}}\cdot\frac{1}{\text{s}}=1\frac{\text{m}}{\text{s}^{2}}$
I to co nam wyszło, czyli $1\frac{\text{m}}{\text{s}^{2}}$ jest właśnie przyspieszeniem mojego roweru. Informuje nas ono o tym, że w ciągu każdej sekundy rower jedzie o 1 metr na sekundę szybciej.
Czym jest przyspieszenie? - zabawa z symbolami
Udało nam się to ogarnąć na przykładowych liczbach. Teraz przyszedł czas żeby wprowadzić literki.

Kiedy liczyliśmy o ile metrów na sekundę przyspieszył rower, to policzyliśmy zmianę szybkości roweru, co możemy oznaczyć jako $\Delta v$ i obliczyliśmy to odejmując od szybkości końcowej $v_{k}$ szybkość początkową $v_{0}$
$15\frac{\text{m}}{\text{s}}-5\frac{\text{m}}{\text{s}}=10\frac{\text{m}}{\text{s}}=\Delta v=v_{k}-v_{0}$
A potem tą naszą zmianę szybkości $\Delta v$ podzieliliśmy przez czas $\Delta t$
$\frac{10\frac{\text{m}}{\text{s}}}{10\text{s}}=1\frac{\text{m}}{s^{2}}=a=\frac{\Delta v}{\Delta t}$
Więc nasz wzór na przyspieszenie ma teraz takie dwie postacie, które możemy używać zamiennie
$a=\frac{\Delta v}{\Delta t}=\frac{v_{k}-v_{0}}{\Delta t}$
Czas na wektorki
Pamiętasz, że założyliśmy, że nasz rower porusza się po linii prostej? Niby niepozorne założenie, ale dzięki niemu mogliśmy zignorować wektorki w naszych poprzednich rozważaniach. Ale no nie oszukujmy się, rower ma po to kierownice, żeby skręcać, więc musimy to uwzględnić.

Na szczęście nie zmienia to aż tak dużo. Teraz po prostu nasza zmiana prędkości będzie wektorem $\Delta\vec{v}$ i będzie ona obliczana jako prędkość końcowa $\vec{v}_{k}$ minus prędkość początkowa $\vec{v}_{0}$
$\Delta\vec{v}=\vec{v}_{k}-\vec{v}_{0}$
I właśnie to będziemy dzielić przez czas $\Delta t$. Ale ponieważ dzielimy wektor przez liczbę, to wynikiem będzie też wektor, u nas wektor przyspieszenia $\vec{a}$
$\vec{a}=\frac{\Delta\vec{v}}{\Delta t}=\frac{\vec{v}_{k}-\vec{v}_{0}}{\Delta t}$
I to co teraz uzyskaliśmy jest naszymi wzorami na przyspieszenie. Prościto, co nie?
Zaskakujące własności takiego przyspieszenia
To jeżeli dołożenie wektorów to taka prosta sprawa, to czy one są w ogóle nam potrzebne? Okazuje się, że ta na pozór niewielka zmiana, powoduje duże zmiany. Jak wiesz, wektor charakteryzuje się nie tylko długością, ale i kierunkiem i zwrotem (jak nie wiesz, to cho tu). A więc kiedy mamy nawet dwa wektory o tej samej długości, ale o innych kierunkach to możemy zapisać coś takiego jak na rysunku
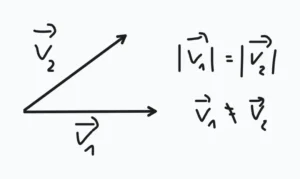
A skoro jeden wektor i drugi nie są identyczne, to jak je odejmiemy to zamiast zera dostaniemy taki wektorek jak na rysunku tutaj
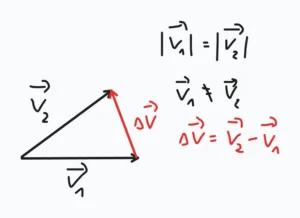
Żeby to jeszcze wyraźniej zobaczyć, to załóżmy, że:
– wektor prędkości początkowej to $\vec{v}_{0}=[5,0]\frac{\text{m}}{\text{s}}$,
– wektor prędkości końcowy jest równy $\vec{v}_{k}=[0,5]\frac{\text{m}}{\text{s}}$.
Spójrz, że oba wektory mają tą samą długość. Sprawdźmy jaka będzie zmiana prędkości $\Delta\vec{v}$ według naszej definicji
$\Delta\vec{v}=\vec{v}_{k}-\vec{v}_{0}$
$\Delta\vec{v}=\vec{v}_{k}-\vec{v}_{0}=[0,5]\frac{\text{m}}{\text{s}}-[5,0]\frac{\text{m}}{\text{s}}$
Kiedy odejmujemy wektory, to od pierwszej składowej odejmujemy pierwszą, a od drugiej drugą
$\Delta\vec{v}=[0-5,5-0]\frac{\text{m}}{\text{s}}=[-5,5]\frac{\text{m}}{\text{s}}$
Czyli wyraźnie widzimy, że zmiana prędkości $\Delta\vec{v}$ nie jest zerowa, pomimo, że wartość prędkości się nie zmieniła. A skoro zmiana prędkości $\Delta\vec{v}$ nie jest zerowa, to i przyspieszenie nie będzie zerowe. Czyli, nasze przyspieszenie zawiera informacje nie tylko o tym, czy ciało zwalnia, bądź przyspiesza, ale też o tym, że skręca. Zaskakująca akcja, co nie?
Podsumowując
Jakbym miał powiedzieć o przyspieszeniu tak w streszczeniu, to brzmiało by ono tak.
Przyspieszenie $\vec{a}$ mówi nam jak szybko zmienia się prędkość ciała, z naciskiem na słowo prędkość – czyli wektor. A więc zarówno o tym jak zmienia się szybkość poruszania ciała, jak i to, jak ciało skręca. A i żebym nie zapomniał, jednostką przyspieszenia jest $\frac{\text{m}}{\text{s}^2}$.
To by było dzisiaj na tyle. Niech kinematyka będzie z tobą i pamiętaj, unikaj zjeżdżalnio tarek.
A jeżeli przyspieszenie ci już nie straszne, to spróbuj sił w quizie poniżej.

