Przemieszczenie i droga - zadania
Zadania z przemieszczenia i drogi
Jeżeli chcesz zacząć od przerobienia teorii o przemieszczeniu i drodze, bądź chcesz sobie odświeżyć tą wiedzę, to super trafiłeś. Wystarczy kliknąć w zielonego poniżej
A jeśli teoria jest ci znana, to od razu wskakujmy do działania, robiąc zadania z przemieszczenia i drogi.
Każde zadanie otrzymało ode mnie oznaczenie trudności według skali:
* łatwe
** średnie
*** trudne
**** bardzo trudne
Ponadto w każdym z nich znajdziesz: treść, podpowiedzi, odpowiedź oraz filmik z rozwiązaniem.
Mam nadzieję, że zadania te pomogą lepiej ci zrozumieć fizykę no i powodzenia!
Zadanie 1. *
Królik Anastazy został złapany przez Stefana (szalonego naukowca) i zredukowany do punktu materialnego umieszczonego w punkcie (0,0). Przerażony Anastazy postanowił uciec i przemieścił się o $\Delta\vec{r}=[2,0]$. Jaki jest obecny wektor położenia królika? [podpowiedź + odpowiedź + rozwiązanie]
Ps. To wcale nie jest tak jak myślisz. Wcale nie mam na imię Stefan, nie włamałem się na tę stronę i nie próbuje znaleźć uciekiniera.
Zadanie 2. *
Czy znasz legendę o półwidzialnym punkcie materialnym, który miał swój dom w początku układu współrzędnych, czyli w punkcie (0,0), ale jednego dnia przepadł? Ludzie szukali go długo, aż w końcu, ktoś odnalazł wyskrobaną informację na wewnętrznej stronie drzwi od szafy. Informacja ta wyglądała tak: $\Delta\vec{r}=[0,5]$. Jeżeli założylibyśmy, że znaleziona na drzwiach informacja, to wektor przemieszczenia się legendarnego półwidzialnego punktu materialnego, to jaki jest jego wektor położenia końcowego i jaką drogę on pokonał? Załóżmy, że punkt szedł po najkrótszej możliwie trasie, czyli po linii prostej. [podpowiedź + odpowiedź + rozwiązanie]
Zadanie 3. *
Za lasami, za górami, mieszkał osioł, punktem materialnym zwany. Osioł ten chatkę miał niepospolita, bo ulokowaną w miejscu (0,0) układu współrzędnych. Lecz zwierzak świata był ciekaw. Sprzedał swe podkówki i za otrzymane pieniądze kupił mapę od wędrownego handlarza. Spakował się i ruszył w nieznane. Brzmi ciekawie, prawda? Dla mnie owszem, dlatego poleciłem go śledzić i teraz słuchaj uważnie. Mój agent powiedział mi, że osiołek przemieścił się o wektor $\Delta\vec{r}=[-2,4]$. Powiedz mi, jaki jest obecny wektor położenia osiołka i w jakiej odległości jest od nas, jeżeli my jesteśmy u niego w domu. Oczywiście, załóżmy, że osiołek jest prawdziwym punktem materialnym. [podpowiedź + odpowiedź + rozwiązanie]
Zadanie 4. **
Szybkonogi Mike wystartował w biegu dobroczynnym. Start wyścigu był ulokowany w punkcie (4,-2). Uczestnicy, w tym Mike, biegną po linii prostej do mety. Tylko gdzie jest ta meta, jeżeli uczestnicy mają przemieścić się o wektor $\Delta\vec{r}$ = [-10,8]? Znajdź wektor położenia mety oraz oblicz, jaką drogę musi pokonać Mike, żeby dotrzeć od startu do mety. [podpowiedź + odpowiedź + rozwiązanie]
Zadanie 5. ***
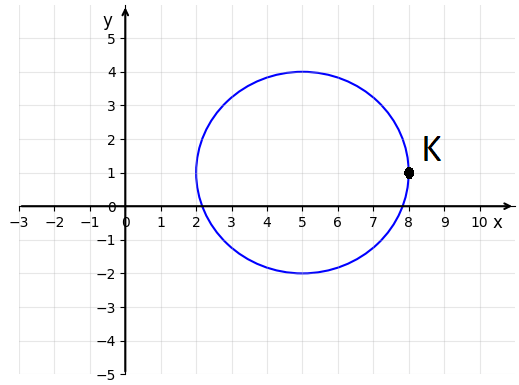
Światowy dzień dinozaurów jest obchodzony 26 lutego. Z tej okazji Karol postanowił przebrać się za tyranozaura rexa i zadriftować na swojej elektrycznej hulajnodze. Jako miejsce driftu wybrał rondo pod blokiem. Podczas driftu, Karol wpadł w niekontrolowany poślizg i po przejechaniu połowy obwodu ronda wypadł z niego. Na szczęście nic mu się nie stało. Poniżej widzimy wspomniane rondo w uproszczonej formie (załóżmy, że ruch Karola odbywał się po okręgu). Literą K oznaczono początkowe położenie Karola, czyli moment kiedy dopiero wjeżdża na rondo. Jaki jest wektor przemieszczenia Karola, od miejsca oznaczonego punktem K, do miejsca, gdzie wypadł z ronda? Jaka jest długość wektora przemieszczenia? Jaką drogę podczas tego ruchu pokonał? [podpowiedź + odpowiedź + rozwiązanie]
Zadanie 6. ***
Gdyby Alfred nie doznał kontuzji w ’98 roku, dziś byłby najbardziej znanym hokeista w historii. Niestety kontuzji nie cofniemy i dlatego dziś Alfred jest trenerem damskiej drużyny hokejowej w Radomiu. Lubi tę pracę, ale złość z powodu kontuzji nadal w nim siedzi. Podczas wczorajszego treningu częściowo ją wyładował pchając krążek po lodowisku z całej siły. Krążek pokonał drogę wzdłuż linii prostej i zatrzymał się 30 metrów od Alfreda. Jaki jest wektor przemieszczenia krążka, jeżeli założymy, że ruch odbywał się w pierwszej ćwiartce układu kartezjańskiego oraz krążek poruszał się po prostej nachylonej pod kątem $\frac{\pi}{6}$ radiana do osi odciętych? [podpowiedź + odpowiedź + rozwiązanie]
Zadanie 7. ***
Bieg na orientacje polega na pokonywaniu dystansu między jednym punktem kontrolnym, a drugim, a potem trzecim itd. Jaś postanowił wziąć w nim udział. Bieg zaczął się w punkcie (-3,4). Pierwszy punkt kontrolny miał miejsce w punkcie (-3, -3), drugi w punkcie (4,-3), trzeci w punkcie (1, 5), a meta znajdowała się na współrzędnych takich samych jak start. Pomiędzy kolejnymi punktami trasa biegła w linii prostej. Oblicz:
a) wektor przemieszczenia Jasia od startu do mety i długość drogi jaką podczas tego ruchu pokonał,
b) wektor przemieszczenie Jasia od pierwszego punktu kontrolnego do trzeciego i długość tego wektora. [podpowiedź + odpowiedź + rozwiązanie]
Zadanie 8. ***
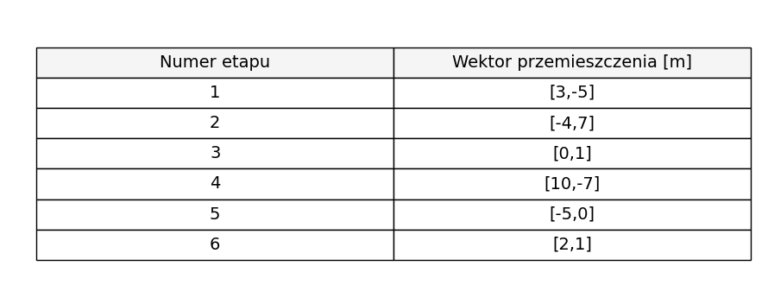
Pszczoła Stefania wyleciała z ula położonego w punkcie (1,-1) układu współrzędnych. Następnie zaczęła latać od kwiatka do kwiatka. Pewien człowiek obserwował lot Stefani i w tabelce (patrz niżej) zebrał w jaki sposób przemieszczała się. Całą podróż podzielił na etapy, odpowiadającym lotom do kolejnych kwiatów. Powiedz jakie są współrzędne ostatniego kwiatu, który odwiedziła. [podpowiedź + odpowiedź + rozwiązanie]
A jeżeli chcesz od razu wskoczyć do playlisty na YouTubie na której rozwiązuje zadania z tego tematu to klikaj tutaj.

